Odmah da znate, Gomboc je čudna stvar. Izgleda kao jaje sa oštrim ivicama, a kad ga odložite, počinje da se migolji i valja oko sebe kao da ima sopstvenu volju. Do nedavno niko nije znao da li Gomboc uopšte postoji. Čak i sada, Gabor Domokos, jedan od njihovih pronalazača, računa da u nekom smislu Gomboc jedva da uopšte postoji.

Šta je to onda Gomboc i šta ga čini posebnim?

Zamislite obično jaje. Možete ga odložiti na bok, malo će se zakotrljati, ali na kraju će se umiriti. Možete ga i gurnuti, opet će se smiriti. Uz puno vještine možete ga uravnotežiti i na jednom od dva kraja: nije lako, a ako se uspijete, neće dugo trajati. Najmanji poremećaj učiniće da se prevrne.

Dva vrha jajeta su poznata kao nestabilne tačke ravnoteže. „Ravnoteže“ jer na njima možete uravnotežiti jaje i „nestabilne“ jer će jaje pasti na najmanji dodir. Tačke oko tijela jajeta na kojima ono snažno balansira nazivaju se tačke stabilne ravnoteže.

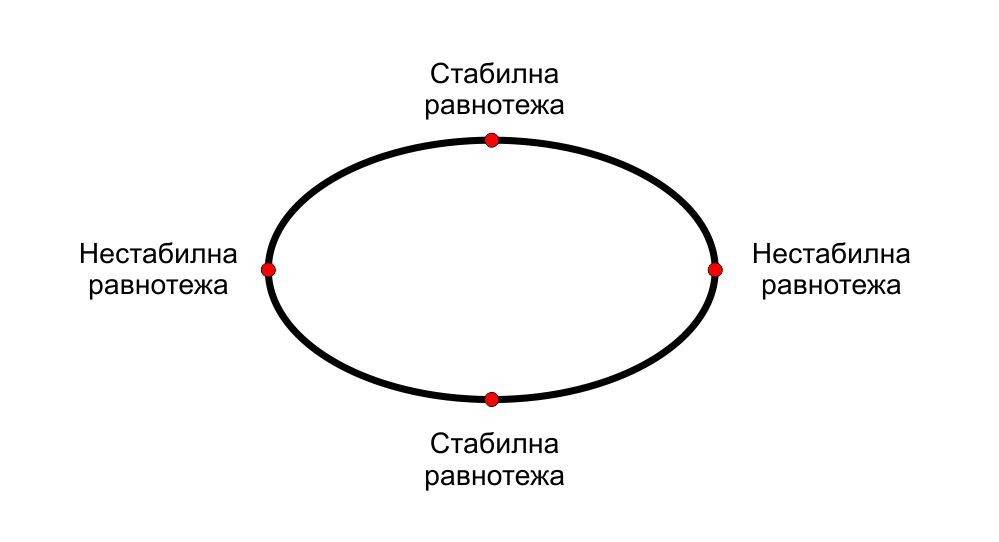
Kakvu kombinaciju tačaka ravnoteže može imati objekat? Lakše je razmišljati u dvije dimenzije. Kvadrat ima četiri stabilne tačke ravnoteže, središta njegovih stranica i možete ga uravnotežiti u tim tačkama. Takođe, na svojim uglovima ima četiri nestabilne tačke ravnoteže. Trokut ima tri stabilne tačke u središtima stranica i po tri nestabilne na uglovima. Elipsa, koja je pomalo slična dužinskom presjeku jajeta, ima dvije stabilne tačke ravnoteže u središtima svoje duge „stranice“ i dvije nestabilne na krajevima. 

Postavlja se pitanje, postoji li dvodimenzionalni oblik koji je konveksan (nema ispupčenja prema unutra) i homogen (materijal od kojeg je napravljen je jednoličan u cjelosti bez dodatka tegova) i koji ima samo jednu stabilnu i jednu nestabilnu tačku ravnoteže? Odgovor je „ne". Možete dobiti neku ideju o tome kako se osloboditi jedne od nestabilnih tačaka ravnoteže elipse. Da biste to uradili, morali biste na neki način izravnati kraj elipse, stvarajući još jednu stabilnu ravnotežu u procesu. Postoji rigorozan dokaz za ovu činjenicu koji pokazuje da bi postojanje jedne stabilne i jedne nestabilne tačke ravnoteže postavilo nemoguće zahtjeve za težište oblika.

Činilo se da je nešto slično tačno i u tri dimenzije, pa su matematičari prirodno pretpostavili da ne postoji trodimenzionalni konveksni i homogeni oblik sa samo jednom stabilnom i jednom nestabilnom tačkom ravnoteže. Mnogi su pokušali da to dokažu, ali nisu uspjeli. Drugi su polako dolazili do ideje da bi takav objekat ipak mogao postojati. Među njima je bio i Mađar Gabor Domokos koji je ovom predmetu, ukoliko postoji, dao ime. Nazvao ga je Gomboc. Domokos se silno trudio da matematički konstruiše Gomboc i dokaže da on postoji, ali u početku je doživio neuspjeh, kao što oni koji ne vjeruju u Gomboc nisu uspeli da dokažu njegovo nepostojanje. Mađar je onda pristupio nečemu što je za matematičare drastična mjera. Na odmoru na grčkom ostrvu on i njegova supruga sakupili su i pregledali 2000 akmenčića na plaži u nadi da bi se neki mogao ponašati kao Gomboc. Bio je to uzaludan napor. „Naučili smo vrlo zanimljive stvari sa tačke gledišta kamenčića, ali ništa sa gledišta Gomboca“, kaže Domokos. "Bili smo umorni i depresivni. Kada smo pogledali ove kamenčiće, stekli smo osećaj da, čak i ako biste otišli ​​na sva druga grčka ostrva, nikada ne bi pronašli kamenčić koji se ponaša kao Gomboc. Ali zašto ne bi? Ako ova vrsta šljunka ne ne postoji, onda za to mora postojati matematički razlog. "

Ova linija razmišljanja dovela je do važnog zaključka: Domokos i njegov kolega Peter Varkoni shvatili su da Gomboc, ako postoji, ne može biti vrlo ravan ili vrlo tanak. Ravni objekat, poput frizbija, uglavnom ima dvije strane i u svakoj će biti po jedna stabilna tačka ravnoteže - to je jedna stabilna ravnoteža previše. Tanak predmet, poput olovke, na svoja dva vrha obično će imati dvije nestabilne tačke ravnoteže, pa ne može biti Gomboc.

 Domokos i Varkoni su svoju intuiciju precizirali davanjem formalne matematičke definicije onoga što podrazumijevaju da je ravno i tanko, od kojih se svaka mjeri brojem većim ili jednakim 1. Zatim su dokazali da Gombocova ravnost i tankost moraju biti jednake 1 , odnosno obje vrijednosti moraju biti što je moguće manje.

Rezultat daje određeni uvid u to zašto se Gomboc klati na ivici postojanja. Ako napravite Gomboc samo malo tanjim ili ravnijim, tada njegove vrijednosti ravnosti i tankoće više nisu minimalne. Prema rezultatima, predmet prestaje da bude Gomboc kada stekne dodatne tačke ravnoteže ili je prestane da bude konveksan.

Osetljivost Gomboca na promjene znači da kamenčić sličan Gombocu može postojati samo kratko vrijeme na morskoj obali, dok se ne počne sudarti sa drugim kamenčićima,što bi narušilo njegov jedinstveni oblik. "To je temeljno pitanje", kaže Domokos, "na koje očekujete jasan odgovor: nešto bi trebalo ili da postoji ili da ne postoji. Ali u slučaju Gomboca, odgovor je da postoji, ali jedva. Ako ako ga ispustite, on prestaje da bude ono što je bio, pa je fizički to vrlo krhko postojanje “.

Objasnivši tako zašto nisu uspjeli da pronađu Gomboc na plaži, Domokos i Varkonii su potegli novu nadu i isprobali novu liniju napada u potrazi za dokazom o njegovom postojanju. Na kraju su i uspjeli, precizirajući tačno kako Gomboc treba da izgleda. Čak su ga i napravili: kada ga spustite, on izvodi čudan ples koji se previja, valjajući se dok se ne zaustavi u svojoj stabilnoj tački ravnoteže.