Одмах да знате, Гомбоц је чудна ствар. Изгледа као јаје са оштрим ивицама, а кад га одложите, почиње да се мигољи и ваља око себе као да има сопствену вољу. До недавно нико није знао да ли Гомбоц уопште постоји. Чак и сада, Габор Домокос, један од њихових проналазача, рачуна да у неком смислу Гомбоц једва да уопште постоји.

Шта је то онда Гомбоц и шта га чини посебним?

Замислите обично јаје. Можете га одложити на бок, мало ће се закотрљати, али на крају ће се умирити. Можете га и гурнути, опет ће се смирити. Уз пуно вјештине можете га уравнотежити и на једном од два краја: није лако, а ако се успијете, неће дуго трајати. Најмањи поремећај учиниће да се преврне.

Два врха јајета су позната као нестабилне тачке равнотеже. „Равнотеже“ јер на њима можете уравнотежити јаје и „нестабилне“ јер ће јаје пасти на најмањи додир. Тачке око тијела јајета на којима оно снажно балансира називају се тачке стабилне равнотеже.

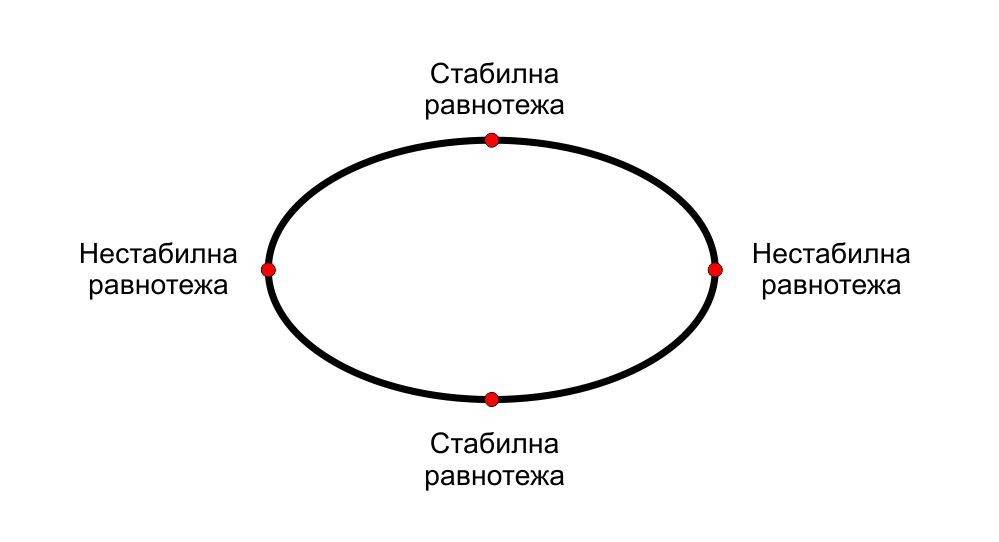
Какву комбинацију тачака равнотеже може имати објекат? Лакше је размишљати у двије димензије. Квадрат има четири стабилне тачке равнотеже, средишта његових страница и можете га уравнотежити у тим тачкама. Такође, на својим угловима има четири нестабилне тачке равнотеже. Трокут има три стабилне тачке у средиштима страница и по три нестабилне на угловима. Елипса, која је помало слична дужинском пресјеку јајета, има двије стабилне тачке равнотеже у средиштима своје дуге „странице“ и двије нестабилне на крајевима. 

Поставља се питање, постоји ли дводимензионални облик који је конвексан (нема испупчења према унутра) и хомоген (материјал од којег је направљен је једноличан у цјелости без додатка тегова) и који има само једну стабилну и једну нестабилну тачку равнотеже? Одговор је „не". Можете добити неку идеју о томе како се ослободити једне од нестабилних тачака равнотеже елипсе. Да бисте то урадили, морали бисте на неки начин изравнати крај елипсе, стварајући још једну стабилну равнотежу у процесу. Постоји ригорозан доказ за ову чињеницу који показује да би постојање једне стабилне и једне нестабилне тачке равнотеже поставило немогуће захтјеве за тежиште облика.

Чинило се да је нешто слично тачно и у три димензије, па су математичари природно претпоставили да не постоји тродимензионални конвексни и хомогени облик са само једном стабилном и једном нестабилном тачком равнотеже. Многи су покушали да то докажу, али нису успјели. Други су полако долазили до идеје да би такав објекат ипак могао постојати. Међу њима је био и Мађар Габор Домокос који је овом предмету, уколико постоји, дао име. Назвао га је Гомбоц. Домокос се силно трудио да математички конструише Гомбоц и докаже да он постоји, али у почетку је доживио неуспјех, као што они који не вјерују у Гомбоц нису успели да докажу његово непостојање. Мађар је онда приступио нечему што је за математичаре драстична мјера. На одмору на грчком острву он и његова супруга сакупили су и прегледали 2000 акменчића на плажи у нади да би се неки могао понашати као Гомбоц. Био је то узалудан напор. „Научили смо врло занимљиве ствари са тачке гледишта каменчића, али ништа са гледишта Гомбоца“, каже Домокос. "Били смо уморни и депресивни. Када смо погледали ове каменчиће, стекли смо осећај да, чак и ако бисте отишли ​​на сва друга грчка острва, никада не би пронашли каменчић који се понаша као Гомбоц. Али зашто не би? Ако ова врста шљунка не не постоји, онда за то мора постојати математички разлог. "

Ова линија размишљања довела је до важног закључка: Домокос и његов колега Петер Варкони схватили су да Гомбоц, ако постоји, не може бити врло раван или врло танак. Равни објекат, попут фризбија, углавном има двије стране и у свакој ће бити по једна стабилна тачка равнотеже - то је једна стабилна равнотежа превише. Танак предмет, попут оловке, на своја два врха обично ће имати двије нестабилне тачке равнотеже, па не може бити Гомбоц.

 Домокос и Варкони су своју интуицију прецизирали давањем формалне математичке дефиниције онога што подразумијевају да је равно и танко, од којих се свака мјери бројем већим или једнаким 1. Затим су доказали да Гомбоцова равност и танкост морају бити једнаке 1 , односно обје вриједности морају бити што је могуће мање.

Резултат даје одређени увид у то зашто се Гомбоц клати на ивици постојања. Ако направите Гомбоц само мало тањим или равнијим, тада његове вриједности равности и танкоће више нису минималне. Према резултатима, предмет престаје да буде Гомбоц када стекне додатне тачке равнотеже или је престане да буде конвексан.

Осетљивост Гомбоца на промјене значи да каменчић сличан Гомбоцу може постојати само кратко вријеме на морској обали, док се не почне сударти са другим каменчићима,што би нарушило његов јединствени облик. "То је темељно питање", каже Домокос, "на које очекујете јасан одговор: нешто би требало или да постоји или да не постоји. Али у случају Гомбоца, одговор је да постоји, али једва. Ако ако га испустите, он престаје да буде оно што је био, па је физички то врло крхко постојање “.

Објаснивши тако зашто нису успјели да пронађу Гомбоц на плажи, Домокос и Варконии су потегли нову наду и испробали нову линију напада у потрази за доказом о његовом постојању. На крају су и успјели, прецизирајући тачно како Гомбоц треба да изгледа. Чак су га и направили: када га спустите, он изводи чудан плес који се превија, ваљајући се док се не заустави у својој стабилној тачки равнотеже.